Question 5 (Fill-In-The-Blank Worth 1 points) (05.05 MC) A system of equations is shown below: 6x - 5y = 5 , 3x + 5y = 4 The x-coordinate of the solution to this system of equat…

Question

asked Feb 20, 2021 95.0k views

2 Answers

Avjol Sakaj · Answer 1 · 2021-02-26T16:41:15+0000

Answer:

The x-coordinate of the solution to this system of equations is 1.

Explanation:

Given,

$6x - 5y = 5\\\\3x + 5y = 4$

We have to find out the x-coordinate of the equation.

Solution,

Let
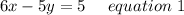
$6x-5y=5\ \ \ \ equation\ 1$

Again let
$3x+5y=4\ \ \ \ \ equation \ 2$

Now using elimination method we will solve the equations.

For this we will add equation 1 and equation 2 and get;

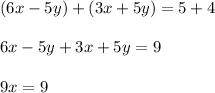
$(6x-5y)+(3x+5y)=5+4\\\\6x-5y+3x+5y=9\\\\9x=9$

Now on dividing both side by '9' we get;

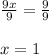
$(9x)/(9)=(9)/(9)\\\\x=1$

Hence The x-coordinate of the solution to this system of equations is 1.