Question

ill has just gotten out of her car in the grocery store parking lot. The parking lot is on a hill and is tilted 3 degrees. Fifty meters downhill from Jill, a little old lady lets go of a fully loaded shopping cart. The cart, with frictionless wheels, starts to roll straight downhill. Jill immediately starts to sprint after the cart with her top acceleration of 2.0m/s2.How far has the cart rolled before Jill catches it?

Answer 1

`t=25.6446\ s`

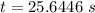
is the time after which Jill will be able to catch the cart.

Step-by-step explanation:

Given:

• angle of inclination,
  `\theta=3\ ^(\circ)`

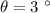
• height of the cart from the level ground,
  `h=50\ m`

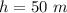
• acceleration of Jill,
  `a=2\ m.s^(-2)`

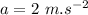
Now the component of gravity acting on the cart along the inclined plane:

`g'=g.sin\ \theta`

`g'=9.8* sin\ 3^(\circ)`

`g'=0.5129\ m.s^(-2)`

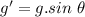
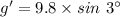
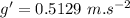
Time taken by Jill to reach this speed:

`v=u+a.t`

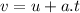
where:

t = time taken

u = initial velocity = 0

`51.289=0+2* t`

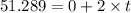
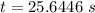`t=25.6446\ s` is the time after which Jill will be able to catch the cart.