Question

Identify az of this sequence: 0.25, 0.5, 0.75, 1, 1.25. 1.5

Answer 1

Answer is [C] 0.75 to 1.0

Explanation:

Hope this helps :)

Answer 2

Question:

Identify a3 of this sequence: 0.25, 0.5, 0.75, 1, 1.25, 1.5,...a3=

Answer:

The third term of sequence is 0.75

`a_3 = 0.75`

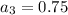
Solution:

Given that, sequence is:

0.25, 0.5, 0.75, 1, 1.25. 1.5

Let us find the difference between terms

`0.5 - 0.25 = 0.25\\\\0.75-0.5 = 0.25\\\\1.25-1=0.25\\\\1.5-1.25=0.25`

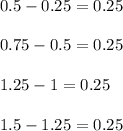
This is a arithmetic sequence

Because the difference between any term and its immediately preceding term is always 0.25

In a arithmetic sequence,

`a_1 = \text{ first term of sequnece }\\\\a_2 = \text{second term of sequnce }\\\\a_3 = \text{third term of sequnece }\\\\a_n = \text{ nth term of sequnce }`

Thus, in the sequence 0.25, 0.5, 0.75, 1, 1.25. 1.5

`a_3 = \text{ third term } = 0.75`

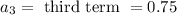
Thus the third term of sequence is 0.75