Question

For the data set: 0.09, 0.10, 0.11, 0.13, 0.09, 0.11, 0.10, 0.07 To obtain information of the precision of the data set the standard deviation would be:

a. 0.018
b. 0.022
c. 0.0166
d. 0.01

Answer 1

Option A is correct (0.018)

S.D≅0.018

Step-by-step explanation:

Option A is correct (0.018)

General Formula for Standard Deviation is:

`Standard\ Deviation=\sqrt{(\sum_(i=1)^(n)(x_(i)-\bar x)^2)/(n-1)}`

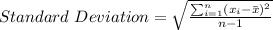
Where:

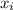`x_(i)` is the data value

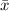`\bar x` is the mean/average of data

n is the total number of data elements

Calculating
`\sum_(i=1)^(n)(x_(i)-\bar x)^2}`

`\bar x=(0.09+0.10+ 0.11+ 0.13+ 0.09+ 0.11+ 0.10+0.07)/(8) \\\bar x=0.1`

`\sum_(i=1)^(n)(x_(i)-\bar x)^2}=(0.09-0.1)^2+(0.1-0.1)^2+(0.11-0.1)^2+(0.13-0.1)^2+(0.09-0.1)^2+(0.11-0.1)^2+(0.1-0.1)^2+(0.07-0.1)^2\\\sum_(i=1)^(n)(x_(i)-\bar x)^2}=2.2*10^(-3)`

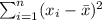
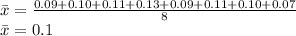
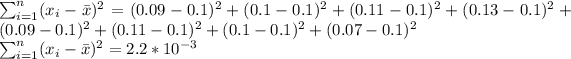
Calculating n-1:

Total number of terms=8

n-1=8-1=7

Standard Deviation is:

`S.D=\sqrt{(2.2*10^(-3))/(7)}\\S.D=0.0177`

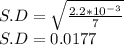
S.D≅0.018