Question

Write the equation in vertex form for the parabola with focus (0,5) and directrix y=

–
5.
Simplify any fractions.

Answer 1

Answer:
`x^(2) = 20y`

Explanation:

The directrix given is vertical , so we will use the formula :

`(x-h)^(2)=4p(y-k)`

P is the distance between the focus , that is 5 - 0 = 5

Therefore : p = 5

(h,k) is the mid point between the focus and the directrix , that is

(h,k) =
`((x_(1)+x_(2) )/(2),(y_(2)+y_(1))/(2))` =
`((0+0)/(2) , (5-5)/(2))` =
`(0,0)`

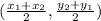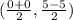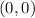
Therefore:

h =0

k = 0

substituting into the formula : we have

`(x-h)^(2)=4p(y-k)`

`(x-0)^(2)` = 4(5)(
`y-0)`

`x^(2) = 20y`

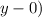
Therefore : the equation in vertex form is
`x^(2) = 20y`