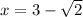Answer:
The solved expression is
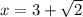 and
and
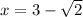
Therefore
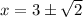
Explanation:
Given quadratic equation is
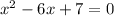
To solve the given equation by using completing the square :
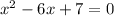
Rewritting the above equation as below :
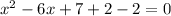

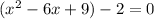
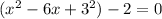
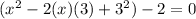 ( it is of the form of
( it is of the form of
 heere a=x and b=3 )
heere a=x and b=3 )


Taking square root on both sides we get
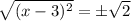
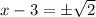
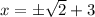
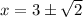
Therefore
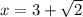 and
and