Answer:
A. Graphing (an equation) point-by-point. B. Function. C. Domain. D. Range (sometimes it is called Codomain). E. One, one.
Explanation:
A. Graphing (an equation) point-by-point.
The process of graphing the set of points that make the equation true can be called a point-by-point graphing or simply graphing an equation. An equation can be a line, a circle, a parabola or other algebraic equations. In a simple case like the equation:
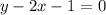 (1)
(1)
We need to solve the equation for x and y, and we know that y can be expressed as:
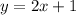 (2)
(2)
Well, we know that all possible values for solving this equation for x are:
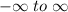
And, as it can be seen in equation (2), the possible values for y are also:
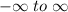
But they are defined by the rule defined in this equation (2).
So, the set of points that make the equation (1) true are all possible Real values. Of course, we do not need to plot any point on a grid but only two pairs of points (x1, y1) and (x2, y2) from the set of solutions to equation (1) to graph this equation since we have here a line. After that, we can connect them with a smooth curve, to then becoming aware that the algebraic equation represents a line.
B. Function. C. Domain. D. Range (sometimes it is called Codomain). E. One, one.
All the remaining options selected can be explained using equation (2).
Equation (2) is a function. The set for the possible values of x are all real numbers:
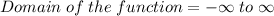
And is called Domain of the function, so it does for the Range of the function (or Codomain), which in this case is also:

However, the values for y (dependent variable) are determined by the independent variable x, according to a specific rule or correspondence (called function), expressed in equation (2).
As an example, selecting some values for x, namely, x={-1, 0, 1}, we can obtain values for y according the correspondence expressed in (2):
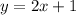
For x = {-1, 0, 1}
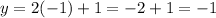
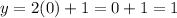
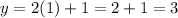
Some values of the Domain (independent variable x) are {-1, 0, 1} from all real numbers for which are associated or are in correspondence to elements of the Range (dependent variable y) {-1, 1, 3}.
Thus, we have a tiny sample of ordered pairs that solve the equation (1): {(-1, -1), (0, 1) and (1, 3)}, that helps to graph the equation point by point.
We can also conclude that there is one element in the Domain that corresponds to a unique element in the Range (or Codomain), that is, for x = -1, there is only y = -1, for x = 0, there is only a y = 1, and so on.