Question

A cone-shaped building has a height of 11.4 meters and a base with a diameter of 12 meters. The building will be filled with road salt that costs $20 per cubic meter. How much will it cost to fill the building with road salt? Use 3.14 for π

Answer 1

The cost to fill the building with road salt is $ 8591.04

Solution:

Given that, A cone-shaped building has a height of 11.4 meters and a base with a diameter of 12 meters

Therefore,

Height = 11.4 meters

diameter = 12 meters

`radius = (diameter)/(2) = (12)/(2) = 6`

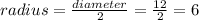
radius = 6 meters

Let us first find the volume of cone

The volume of cone is given as:

`V = (\pi r^2h)/(3)`

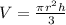
Where, "V" is the volume of cone

"h" and "r" are height and radius of cone

Substituting the given values, we get

`V = (3.14 * 6^2 * 11.4)/(3)\\\\V = 3.14 * 12 * 11.4\\\\V = 429.552`

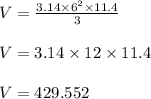
Thus volume of cone is 429.552 cubic meters

The building will be filled with road salt that costs $20 per cubic meter

1 cubic meter = $ 20

Therefore, for 429.552 cubic meters, we get,

`cost = 20 * 429.552\\\\cost = 8591.04`

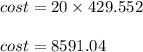
Thus cost to fill the building with road salt is $ 8591.04