Question

Sirius, in Canis Major (the large hunting dog of Orion), is the brightest star in the winter night sky. It has a parallax angle of 0.38 seconds of arc. Orion's other hunting dog, Canis Minor, has as its brightest star Procyon, with a parallax angle of 0.29 seconds of arc. Vega, in Lyra the Lyre (Harp), is the brightest star in the summer night sky. It has a parallax angle of 0.13 seconds of arc. Which of these stars is farthest away? A.Procyon b.Vega c.It cannot be determined from this information alone d.Sirius

Answer 1

Option b

b. Vega

Step-by-step explanation:

The angle due to the change in position of a nearby object against the background stars it is known as parallax (see the image below).

The parallax angle can be used to find out the distance by means of triangulation. Making a triangle between the nearby star, the Sun and the Earth (as is shown in the image below), knowing that the distance between the Earth and the Sun (150000000 Km), is defined as 1 astronomical unit (AU).

`tan(p) = (1AU)/(d)`

Where d is the distance to the star.

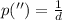`p('') = (1)/(d)` (1)

Equation (1) can be rewritten in terms of d:

`d(pc) = (1)/(p(''))` (2)

Equation (2) represents the distance in a unit known as parsec (pc).

For the case of Sirius (
`p('') = 0.38`):

`d(pc) = (1)/(0.38)`

`d(pc) = 2.63`

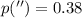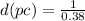
Hence, the object is 2.63 parsecs away from Earth.

For the case of Procyon (
`p('') = 0.29`):

`d(pc) = (1)/(0.29)`

`d(pc) = 3.44`

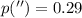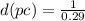
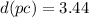
Hence, the object is 3.44 parsecs away from Earth.

For the case of Vega (
`p('') = 0.13`):

`d(pc) = (1)/(0.13)`

`d(pc) = 7.69`

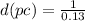
Hence, the object is 7.69 parsecs away from Earth.

Therefore, Vega is the star farther away.

Summary:

Notice how a small parallax angle means that the object is farther away.