Question

This semicircle has a radius of 8cm . What is the area of this figure?​

Answer 1

100.48 cm² ( option 2 )

Explanation:

Given:-

• Radius of semicircle :- 8cm

To find:-

• Area of the figure

Solution:-

Area of semi-circle :-

`(1)/(2) \pi \: r {}^(2)`

1/2 × 3.14 × 8²

`100.48 \: cm {}^(2)`

Answer 2

• 100.48 cm² (Option 2)

⠀

Explanation:

⠀

We know,

`{\longrightarrow \qquad \boldsymbol{\pmb{Area_((semicircle)) = (1)/(2)( \pi {r}^(2) ) }}}`

⠀

Where,

• r is the radius of the semicircle. Here, the radius is 8 cm .

• We will take the value of π as 3.14 .

⠀

Now, Substituting the values in the formula :

⠀

`{\longrightarrow \qquad \rm{{Area_((semicircle)) = \it (1)/(2) * 3.14 * ({8})^(2) }}}`

`{\longrightarrow \qquad \rm{{Area_((semicircle)) = \it (1)/( \cancel2) * 3.14 * \cancel{64} }}}`

⠀

`{\longrightarrow \qquad \rm{{Area_((semicircle)) = \it {1} * 3.14 * 32 }}}`

⠀

`{\longrightarrow \qquad \rm{{Area_((semicircle)) = \it {1} * 100.48 }}}`

⠀

`{\longrightarrow \qquad \boldsymbol{ \pmb{Area_((semicircle)) \approx \it 100.48 }}}`

⠀

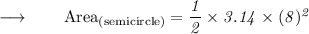
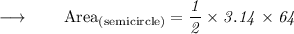
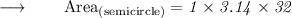
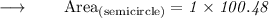
Therefore,

• The area of the semicircle is 100.48 cm² approximately .