Question

To identify a diatomic gas (X2), a researcher carried out the following experiment: She weighed an empty 4.4-L bulb, then filled it with the gas at 1.00 atm and 22.0 ∘C and weighed it again. The difference in mass was 5.1 g . Identify the gas.

Answer 1

Answer : The diatomic gas is nitrogen gas, N₂.

Explanation :

First we have to calculate the moles of gas.

Using ideal gas equation:

`PV=nRT`

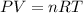
where,

P = Pressure of gas = 1.00 atm

V = Volume of gas = 4.4 L

n = number of moles of gas = ?

R = Gas constant =
`0.0821L.atm/mol.K`

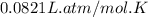
T = Temperature of gas =
`22.0^oC=273+22.0=295.0K`

Putting values in above equation, we get:

`1.00atm* 4.4L=n* (0.0821L.atm/mol.K)* 295.0K`

`n=0.1817mol`

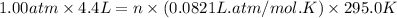
Now we have to calculate the molar mass of gas.

`\text{Molar mass of gas}=\frac{\text{Given mass of gas}}{\text{Moles of gas}}`

`\text{Molar mass of gas}=(5.1g)/(0.1817mol)=28.07g/mol`

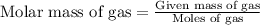
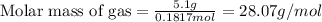
As we are given that the gas is diatomic X₂.

As, 2 atoms of gas X has mass = 28.07 g/mol

So, 1 atom of gas will have mass =
`(28.07)/(2)=14.04g/mol`

From this we conclude that the nitrogen atom has mass of 14.04 g/mol.

Thus, the diatomic gas is nitrogen gas, N₂.