Question

A 16.2 kg person climbs up a uniform ladder with negligible mass. The upper end of the ladder rests on a frictionless wall. The bottom of the ladder rests on a floor with a rough surface where the coefficient of static friction is 0.42 . The angle between the horizontal and the ladder is θ . The person wants to climb up the ladder a distance of 0.9 m along the ladder from the ladder’s foot. 16.2 kg 0.9 m 2 m θ b µ = 0.42 µ = 0 What is the minimum angle θmin (between the horizontal and the ladder) so that the person can reach a distance of 0.9 m without having the ladder slip? The acceleration of gravity is 9.8 m/s 2

Answer 1

To solve this problem we will apply the concepts related to the balance of forces. We will decompose the forces in the vertical and horizontal sense, and at the same time, we will perform summation of torques to eliminate some variables and obtain a system of equations that allow us to obtain the angle.

The forces in the vertical direction would be,

`\sum F_x = 0`

`f-N_w = 0`

`N_w = f`

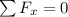
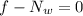
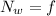
The forces in the horizontal direction would be,

`\sum F_y = 0`

`N_f -W =0`

`N_f = W`

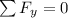
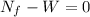
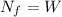
The sum of Torques at equilibrium,

`\sum \tau = 0`

`Wdcos\theta - N_wLsin\theta = 0`

`WdCos\theta = fLSin\theta`

`f = (Wd)/(Ltan\theta)`

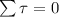
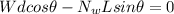
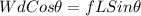
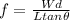
The maximum friction force would be equivalent to the coefficient of friction by the person, but at the same time to the expression previously found, therefore

`f_(max) = \mu W=(Wd)/(Ltan\theta)`

`\theta = tan^(-1) ((d)/(\mu L))`

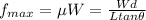
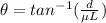
Replacing,

`\theta = tan^(-1) ((0.9)/(0.42*2))`

`\theta = 46.975\°`

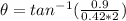
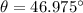
Therefore the minimum angle that the person can reach is 46.9°