Question

Which of the following integrals cannot be evaluated using a simple substitution? (4 points) Select one:

a. the integral of the square root of the quantity x minus 1, dx
b. the integral of the quotient of 1 and the square root of the quantity 1 minus x squared, dx
c. the integral of the quotient of 1 and the square root of the quantity 1 minus x squared, dx
d. the integral of x times the square root of the quantity x squared minus 1, dx

Answer 1

B. and C.

General Formulas and Concepts:

Calculus

Differentiation

• Derivatives
• Derivative Notation

Integration

• Integrals
• Indefinite Integrals
• Integration Constant C

U-Substitution

Explanation:

*Note:

It seems like B and C are both the same answer.

Let's define our answer choices:

a.
`\displaystyle \int {√(x - 1)} \, dx`

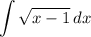
b.
`\displaystyle \int {(1)/(√(1 - x^2))} \, dx`

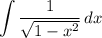
c.
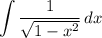
`\displaystyle \int {(1)/(√(1 - x^2))} \, dx`

d.
`\displaystyle \int {x√(x^2 - 1)} \, dx`

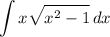
Let's run u-substitution through each of the answer choices:

a.
`\displaystyle u = x - 1 \rightarrow du = dx \ \checkmark`

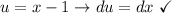
∴ answer choice A can be evaluated with a simple substitution.

b.
`\displaystyle u = 1 - x^2 \rightarrow du = -2x \ dx`

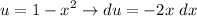
We can see that this integral cannot be evaluated with a simple substitution. In fact, this is a setup for an arctrig integral.

∴ answer choice B cannot be evaluated using a simple substitution.

C.
`\displaystyle u = 1 - x^2 \rightarrow du = -2x \ dx`

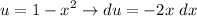
We can see that this integral cannot be evaluated with a simple substitution. In fact, this is a setup for an arctrig integral.

∴ answer choice C cannot be evaluated using a simple substitution.

D.
`\displaystyle u = x^2 - 1 \rightarrow du = 2x \ dx \ \checkmark`

Using a little rewriting and integration properties, this integral can be evaluated using a simple substitution.

∴ answer choice D can be evaluated using a simple substitution.

Out of all the choices, we see that B and C cannot be evaluated using a simple substitution.

∴ our answer choices should be B and C.

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration

Book: College Calculus 10e