Question

A(n) 12500 lb railroad car traveling at 7.8 ft/s couples with a stationary car of 7430 lb. The acceleration of gravity is 32 ft/s 2 . What is their velocity after the collision

Answer 1

To solve this problem we will apply the concepts related to the conservation of momentum. That is, the final momentum must be the same final momentum. And in each state, the momentum will be the sum of the product between the mass and the velocity of each object, then

`\text{Initial Momentum} = \text{Final Momentum}`

`m_1u_1 +m_2u_2 = m_1v_1+m_2v_2`

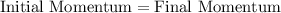
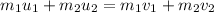
Here,

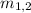`m_(1,2)`= Mass of each object

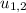`u_(1,2)`= Initial velocity of each object

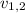`v_(1,2)`= Final velocity of each object

When they position the final velocities of the bodies it is the same and the car is stationary then,

`m_2u_2 = (m_1+m_2)v_f`

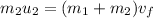
Rearranging to find the final velocity

`v_f = (m_2u_2)/( (m_1+m_2))`

`v_f = ( 12500*7.8)/( 12500+7430)`

`v_f = 4.8921ft/s`

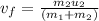
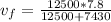
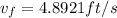
The expression for the impulse received by the first car is

`I = m_1 (v-u)`

`I = (W)/(g) (v-u)`

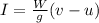
Replacing,

`I = (12500)/(32.2)(4.89-7.8)`

`I = -1129.65lb\cdot s`

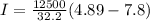
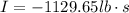
The negative sign show the opposite direction.