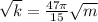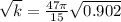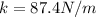Question

An unknown mass of m kg attached to the end of an unknown spring k has a natural frequency of 94cpm. when a 0.453 kg mass is added to m, the natural frequency is lowered to 76.7cpm. determine the unknown mass m and the spring constant k N/m.

Answer 1

To solve this problem we will define the two frequencies given. From there and in international units, we will proceed to clear the variable concerning the spring constant from both equations. We will match the two equations and find the mass. With the mass found we will replace in any of the two system equations and find the spring constant

`f_1 = (1)/(2\pi) (\sqrt{(k)/(m)} ) = 94(cycles)/(minute) * (1 minute)/(60s) = (47)/(30) cycles/s`

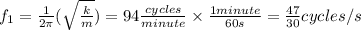
Now

`f_2 = (1)/(2\pi) (\sqrt{(k)/(m+0.453)}) = 76.7(cycles)/(minute) * (1 minute)/(60s) = (767)/(600) cycles/s`

The two equations could be described as:

1)

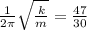
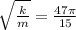
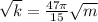
`(1)/(2\pi) \sqrt{(k)/(m)} = (47)/(30)`

`\sqrt{(k)/(m)} = (47\pi)/(15)`

`√(k) = (47\pi)/(15)√(m)`

2)

`(1)/(2\pi) \sqrt{(k)/(m+0.453)}) = (767)/(600)`

`\sqrt{(k)/(m+0.453)} = (767\pi)/(300)`

`√(k) = (767\pi)/(300)√(m+0.453)`

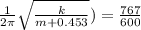
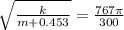
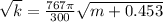
Equation both expression we have that,

`(47\pi)/(15)√(m) = (767\pi)/(300)√(m+0.453)`

`√(m)= (767)/(940) √(m+0.453)`

`m(1-(588289)/(883600)) = (588289)/(883600) * 0.453`

`m = ((588289)/(883600) * 0.453)/((1-(588289)/(883600)))`

`m \approx 0.902kg`

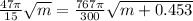
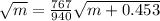
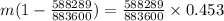
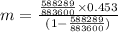
Use one of the formulas from the system

`√(k) = (47\pi)/(15)√(m)`

`√(k) = (47\pi)/(15)√(0.902)`

`k = 87.4N/m`