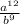Answer:
The answer to your question is the second option
Explanation:
Process
Simplify using exponents laws, first inside the parentheses and then outside the parentheses.
![[(a^(-2)b^(2))/(a^(2)b^(-1)) ]^(-3)](https://img.qammunity.org/2021/formulas/mathematics/high-school/sns133b65jjboyqlbj9hz6ydiii5bw3tub.png)
a) Simplify a
a⁻² a⁻² = a⁻⁴
b) Simplify b
b² b¹ = b³
c) Write the result
![[(b^(3))/(a^(4))]^(-3)](https://img.qammunity.org/2021/formulas/mathematics/high-school/fjkdgvd5k3no39nks6polh7ufbwrrlwhbn.png)
d)
![[(a^(4))/(b^(3))]^(3)](https://img.qammunity.org/2021/formulas/mathematics/high-school/o8twp1znkfv97aq0nbde7x58lusxs96v41.png)
e) Simplify
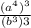
f) Result