Answer:
a) The 95% confidence interval for the population proportion of college students who work to pay for tuition andliving expenses is (0.4239, 0.5161).
b) The 99% confidence interval for the population proportion of college students who work to pay for tuition and living expenses is (0.4094, 0.5306).
c)The margin of error increases as the confidence level increases.
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence interval
, and a confidence interval
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the zscore that has a pvalue of
 .
.
For this problem, we have that:
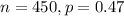
a) Provide a 95% confidence interval for the population proportion of college students who work to pay for tuition andliving expenses.
95% confidence interval
So
 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
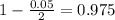 , so
, so
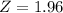 .
.
The lower limit of this interval is:
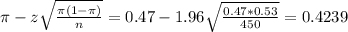
The upper limit of this interval is:
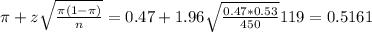
The 95% confidence interval for the population proportion of college students who work to pay for tuition andliving expenses is (0.4239, 0.5161).
b. Provide a 99% confidence interval for the population proportion of college students who work to pay for tuition andliving expenses.
95% confidence interval
So
 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
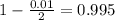 , so
, so
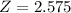 .
.
The lower limit of this interval is:
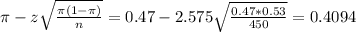
The upper limit of this interval is:
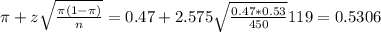
The 99% confidence interval for the population proportion of college students who work to pay for tuition and living expenses is (0.4094, 0.5306).
c What happens to the margin of error as the confidence is increased from 95% to 99%?
The margin of error is the subtraction of the upper end by the lower end of the interval, divided by 2. So
95% confidence interval
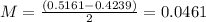
99% confidence interval
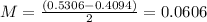
The margin of error increases as the confidence level increases.