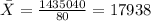Question

A company had 80 employees whose salaries are summarized in the frequency distribution below. Find the

mean salary.
Salary ($) Employees
5,001-10,000 16
10,001-15,000 14
15,001-20,000 15
20,001-25,000 17
25,001-30,000 18

Answer 1

`\bar X = (1435040)/(80)=17938`

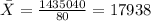
Explanation:

Since we have a groued data for this case we can construct the following table to find the expected value.

Interval Frequency(fi) Midpoint(xi) xi*fi

5001-10000 16 7500.5 120008

10001-15000 14 12500.5 175007

15001-20000 15 17500.5 262507.5

20001-25000 17 22500.5 382508.5

25001-30000 18 27500.5 495009

Total 80 1435040

And we can calculate the mean with the following formula:

`\bar X = (\sum_(i=1)^n f_i x_i)/(n)`

Where
`n=\sum_(i=1)^n f_i = 80`

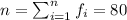
And if we replace we got:

`\bar X = (1435040)/(80)=17938`