To solve this problem we will apply the first law of thermodynamics which details the relationship of energy conservation and the states that the system's energy has. Energy can be transformed but cannot be created or destroyed.
Accordingly, the rate of work done in one cycle and the heat transferred can be expressed under the function,
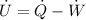
Substitute 1W for
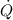 and 1.5 W for
and 1.5 W for
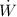
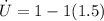
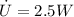
Now calculcate the rate of specific internal energy increase,
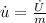
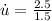
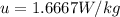
The rate of specific internal energy increase is 1.6667W/kg