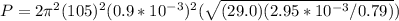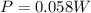Question

A piano wire with mass 2.95 g and length 79.0 cm is stretched with a tension of 29.0 N . A wave with frequency 105 Hz and amplitude 1.80 mm travels along the wire.

(a) Calculate the average power carried by the wave.
(b) What happens to the average power if the wave amplitude is halved?

Answer 1

The concept needed to solve this problem is average power dissipated by a wave on a string. This expression ca be defined as

`P = (1)/(2) \mu \omega^2 A^2 v`

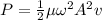
Here,

`\mu` = Linear mass density of the string

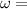`\omega =` Angular frequency of the wave on the string

A = Amplitude of the wave

v = Speed of the wave

At the same time each of this terms have its own definition, i.e,

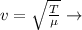`v = \sqrt{(T)/(\mu)} \rightarrow` Here T is the Period

For the linear mass density we have that

`\mu = (m)/(l)`

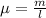
And the angular frequency can be written as

`\omega = 2\pi f`

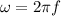
Replacing this terms and the first equation we have that

`P = (1)/(2) ((m)/(l))(2\pi f)^2 A^2(\sqrt{(T)/(\mu)})`

`P = (1)/(2) ((m)/(l))(2\pi f)^2 A^2 (\sqrt{(T)/(m/l)})`

`P = 2\pi^2 f^2A^2(√(T(m/l)))`

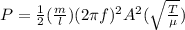
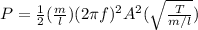
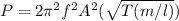
PART A ) Replacing our values here we have that

`P = 2\pi^2 (105)^2(1.8*10^(-3))^2(\sqrt{(29.0)(2.95*10^(-3)/0.79)})`

`P = 0.2320W`

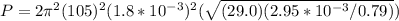
PART B) The new amplitude A' that is half ot the wavelength of the wave is

`A' = (1.8*10^(-3))/(2)`

`A' = 0.9*10^(-3)`

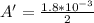
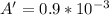
Replacing at the equation of power we have that

`P = 2\pi^2 (105)^2(0.9*10^(-3))^2(\sqrt{(29.0)(2.95*10^(-3)/0.79)})`

`P = 0.058W`