Answer: The density of the given sample of hydrogen gas is 0.061 g/L
Step-by-step explanation:
Assuming ideal gas behavior, the equation follows:
PV = nRT
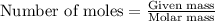
Rearranging the above equation:
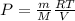
We know that:
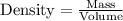
Rearranging the above equation:
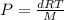 ......(1)
......(1)
We are given:
P = pressure of the gas = 0.799 atm
d = density of hydrogen gas = ?
R = Gas constant =
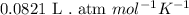
T = temperature of the gas =
![47^oC=[47+273]K=320K](https://img.qammunity.org/2021/formulas/chemistry/college/7cnmypjdh02h1irgbw90ur8mcilqk46l8r.png)
M = molar mass of hydrogen gas = 2 g/mol
Putting values in equation 1, we get:
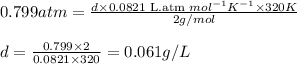
Hence, the density of the given sample of hydrogen gas is 0.061 g/L