Question

A monkey weighs 6.00 x 102 N and swings from vine to vine. As the monkey grabs a new vine, both vines make an angle of 35.0° with the vertical. In such a condition of static equilibrium, what is the net force on the new vine?

Answer 1

To solve this problem we will apply the considerations of equilibrium on a body, we will decompose the tensions into their respective components and apply the sum of forces and solving equations for the given system.

According to the graph, the sum of the horizontal components would be

`\sum T_x = 0`

`TSin35\° -TSin35\° = 0`

`0 = 0`

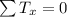
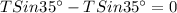
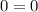
The sum of the vertical components is

`\sum T_y = 0`

`2TCos35\° - mg = 0`

`2TCos35\° = 600N`

`T = (600N)/(2Cos35\°)`

`T = 366.2N`

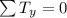
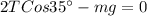
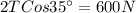
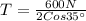
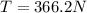
Therefore the net force on the new vine is 366.2N