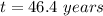Question

A person invests $200 in an account that earns 1.98% annual interest compounded

quarterly. Find when the value of the investment reaches $500.

Answer 1

`t=46.4\ years`

Explanation:

we know that

The compound interest formula is equal to

`A=P(1+(r)/(n))^(nt)`

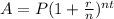
where

A is the Final Investment Value

P is the Principal amount of money to be invested

r is the rate of interest in decimal

t is Number of Time Periods

n is the number of times interest is compounded per year

in this problem we have

`t=?\ years\\P=\$200\\A=\$500\\ r=1.98\%=1.98/100=0.0198\\n=4`

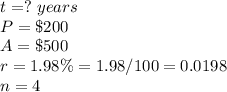
substitute in the formula above

`500=200(1+(0.0198)/(4))^(4t)`

`2.5=(1.00495)^(4t)`

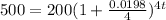
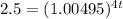
Apply property of exponents

`2.5=[(1.00495)^(4)]^t`

Apply log both sides

`log(2.5)=log[(1.00495)^(4)]^t`

`t=log(2.5)/log[(1.00495)^(4)]`

`t=46.4\ years`