Question is not proper, Proper question is given below;
36% of the beans in Pythagoras's soup are lentils, and 33 1/3% of those lentils are green.
If Pythagoras removes all green lentils from his soup, then x% of the original beans remain. What is x?
Answer:
88% of the original beans remains
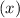 after removing green lentils.
after removing green lentils.
Explanation:
Given:
Let the Original beans be 'n'.
Now given:
36% of the beans in Pythagoras's soup are lentils.
So we can say that;
Amount of lentils =

Also Given:
33 1/3% of those lentils are green
Amount of green lentils =
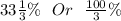
Amount of green lentils =
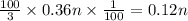
Now we need find the percentage of original beans remain after removing green lentils.
Solution:
percentage of original beans remain ⇒
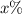
To percentage of original beans remain after removing green lentils we will subtract Amount of green lentils from Original beans and then multiplied by 100.
framing in equation form we get;
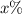 =
=
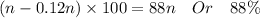
Hence 88% of the original beans remains
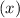 after removing green lentils.
after removing green lentils.