2 Answers

Jack Poulson · Answer 1 · 2021-07-16T14:01:38+0000

Answer:

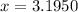
x=3.1950

Explanation:

Given:

The equation to solve is given as:

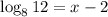
$\log_8 12=x-2$

In order to solve this, we use the base change formula of logarithms.

The base change formula is given as:

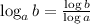
$\log_a b=(\log b)/(\log a)$

Therefore, the equation can be rewritten as:

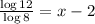
$(\log 12)/(\log 8)=x-2$

Adding 2 on both the sides, we get:

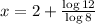
$x=2+(\log 12)/(\log 8)$

Now, we know that,
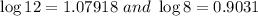
$\log 12=1.07918\ and\ \log 8=0.9031$

Plug in these values and solve for 'x'. This gives,

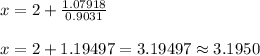
$x=2+(1.07918)/(0.9031)\\\\x=2+1.19497=3.19497\approx3.1950$

Therefore, the value of 'x' is 3.1950 rounded to four decimal places.

Please log in or register to add a comment.