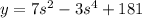Answer:
1)
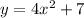
2)
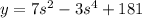
Explanation:
Assuming that our function is
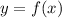 for the first case and
for the first case and
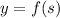 for the second case.
for the second case.
Part 1
We can rewrite the expression like this:
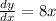
And we can reorder the terms like this:
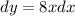
Now if we apply integral in both sides we got:
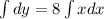
And after do the integrals we got:
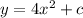
Now we can use the initial condition


And the final solution would be:
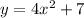
Part 2
We can rewrite the expression like this:

And we can reorder the terms like this:
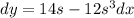
Now if we apply integral in both sides we got:
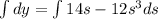
And after do the integrals we got:
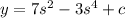
Now we can use the initial condition
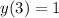
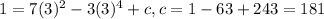
And the final solution would be: