Question

A spacecraft is in a 400-km by 600-km LEO. How long (in minutes) does it take to coast from the perigee to the apogee?

Answer 1

To solve this problem we will use Kepler's third law for which the period is defined as

`T= 2\pi \sqrt{(a^3)/(GM)}`

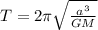
The perigee altitude is the shortest distance between Earth's surface and Satellite.

The average distance of the perigee and apogee of a satellite can be defined as

`a = R+(r_1+r_2)/(2)`

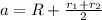
Here,

R = Radius of Earth

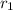`r_1`= Lower orbit

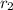`r_2`= Higher orbit

Replacing we have,

`a = 6378.1+(400+600)/(2)= 6878.1km`

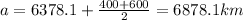
Time Taken to fly from perigee to apogee equals to half of orbital speed is

`t = (T)/(2)`

`t = \pi \sqrt{(a^3)/(GM)}`

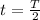
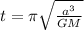
Replacing,

`t =\pi \sqrt{((6878.1*10^3)^3)/((6.67*10^(-11))(6*10^(24)))}`

`t = 2832.79s`

`t = \text{47min 12.8s}`

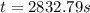
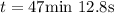
Therefore will take around to 47 min and 12.8s to coast from perigee to the apogee.