Question

Two cyclists leave city at same time, one going east and the other going west. The westbound cyclist bikes 3 mph faster than the eastbound cyclist. If after 6 hours they are 162 miles apart, how fast is each cyclist riding?

Answer 1

Speed of the east bound cyclist is 12 mph and the speed of west bound cyclist is 15 mph.

Solution:

Let us assume that x is speed of slower eastbound cyclist

So, x+3 will be the speed of faster westbound cyclist

We know that distance is the product of speed and time. That is,

`\text{Distance}=\text{Speed}*\text{Time}`

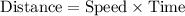
West-bound DATA:

Rate of speed = x+3 mph ; Time = 6 hrs ; distance = 6(x+3) = 6x+18 miles

East-bound DATA:

Rate of speed = x mph ; time = 6 hrs. ; distance = 6x miles

On solving,

Distance apart = 162

`\Rightarrow6x+18+6x = 162`

`\Rightarrow12x=162-18`

`\Rightarrow x=(144)/(12)\rightarrow x=12`

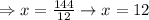
So, the rate of speed of the east bound cyclist is 12 mph and the rate of speed of the west bound cyclist will be
`x+3=12+3=15 \text{ mph}`