Question

A 2.5 kg , 20-cm-diameter turntable rotates at 150 rpm on frictionless bearings. Two 500 g blocks fall from above, hit the turntable simultaneously at opposite ends of a diameter, and stick.

What is the turntable's angular velocity, in rpm, just after this event?

Answer 1

The angular velocity of the turntable just after the blocks hit and stick to it can be calculated using the principle of conservation of angular momentum. The initial angular momentum of the blocks is given by their mass times their initial velocity times their radius of rotation. The final angular momentum of the turntable is equal to the sum of the initial angular momentum of the blocks and the initial angular momentum of the turntable. Therefore, we can calculate the angular velocity of the turntable by dividing the final angular momentum by the moment of inertia of the turntable.

Step-by-step explanation:

The angular velocity of the turntable just after the blocks hit and stick to it can be calculated using the principle of conservation of angular momentum. When the blocks hit the turntable, they transfer their angular momentum to the turntable. The initial angular momentum of the blocks is given by their mass times their initial velocity times their radius of rotation. The final angular momentum of the turntable is equal to the sum of the initial angular momentum of the blocks and the initial angular momentum of the turntable. Therefore, we can calculate the angular velocity of the turntable by dividing the final angular momentum by the moment of inertia of the turntable.

To find the final angular momentum of the turntable, we need to calculate the initial angular momentum of the blocks. Since the blocks fall from above and hit the turntable simultaneously at opposite ends of a diameter, their initial velocity will be equal to their vertical velocity just before they hit the turntable. We can calculate this velocity using the principle of conservation of mechanical energy. The initial potential energy of the blocks is equal to their mass times the acceleration due to gravity times their initial height above the turntable. This potential energy is converted into kinetic energy just before the blocks hit the turntable, according to the law of conservation of mechanical energy. Therefore, we can equate the initial potential energy to the initial kinetic energy to find the initial velocity of the blocks.

Once we have the initial velocity of the blocks, we can calculate their initial angular momentum by multiplying their mass by their initial velocity and the radius of rotation. Adding the initial angular momentum of the blocks to the initial angular momentum of the turntable will give us the final angular momentum of the turntable. Finally, we can divide the final angular momentum by the moment of inertia of the turntable to find the angular velocity of the turntable.

Answer 2

The concepts required to solve this problem are those related to the conservation of the angular momentum and the moment of inertia of the disk. We will begin by calculating the moment of inertia of the disc, then the moment of inertia of the disc after the two two blocks hits and sticks to the edges of the turn table. In the end we will apply the conservation theorem.

The radius is given as,

`R = (20cm)/(2) = 10cm = 0.1m`

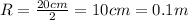
When a block falls from above and sticks to the turn table, the moment inertia of the turntable increases.

Since two blocks are stick to the turn table, the total final moment of inertia of the turntable is the sum moment of inertias of individual turntable, and two blocks.

`I_1 = (1)/(2) MR^2`

`I_1 = (1)/(2) (2.5)(0.1)^2`

`I_1 = 0.0125kg \cdot m^2`

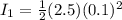
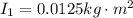
The moment of inertia of each block is

`I_0 = mR^2`

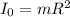
Total moment of inertia of two block is

`I_0' = 2mR^2`

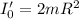
The final moment of inertia of the turn table is

`I_2 = I_1 +I'0`

`I_2 = I_1 +2mR^2`

`I_2 = 0.01kg\cdot m^2 + 2(500*10^(-3)kg)(0.1m)^2`

`I_2 = 0.0225kg\cdot m^2`

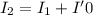
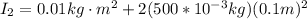
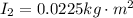
From the conservation of the angular momentum, the initial angular momentum of the system is equal to final angular momentum of the system,

Rearrange the equation we have that

`I_1\omega_2 = I_2\omega_2`

`\omega_2 = (I_1\omega_2)/(I_2)`

`\omega_2 = (0.01*150rpm)/(0.0225)`

`\omega_2 = 66.67rpm`

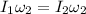
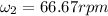
The magnitude of the turntable's angular velocity is 66.67rpm