Answer:
e. 0.0704
Explanation:
We solve this problem building the Venn's diagram of these probabilities.
I am going to say that:
A is the probability that a student plays baseball.
B is the probability that a student plays soccer.
We have that:
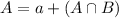
In which a is the probability that a student plays baseball but not soccer and
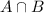 is the probability that a student plays both of these sports.
is the probability that a student plays both of these sports.
By the same logic, we have that:

18% of all students at West Colon High School play baseball and 32% play soccer.
This means that
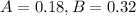
The probability that a student plays baseball given that the student plays soccer is 22%.
This means that

Calculate the probability that a student plays both baseball and soccer.
This is
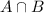

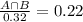

So the correct answer is:
e. 0.0704