Question

The profits of life insurance companies A and B are normally distributed with the same mean. The variance of company B's profit is 2.25 times the variance of company A's profit. The 14th percentile of company A's profit is he same as the pth percentile of company B's profit. Calculate p.

Answer 1

23.58-th

Explanation:

The standard deviation of company B's profit is:

`\sigma_B=√(2.25)\sigma_A`

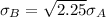
Let X be the profit correspondent to the 14th percentile of company A's profit.

The z-score for 14th percentile of a normal distribution is roughly -1.08.

The z-scores for X in companies A and B are:

`-1.08 = (X-\mu)/(\sigma_a) \\z_B = (X-\mu)/(√(2.25)*\sigma_a)\\z_B=(-1.08)/(√(2.25))\\z_B = -0.72`

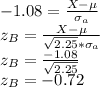
The z-score for X in company B's profit distribution is -0.72, which corresponds to the 23.58-th percentile.