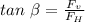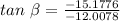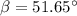Question

Suppose a body has a force of 10 pounds acting on it to the right, 25 pounds acting on it −135° from the horizontal, and 5 pounds acting on it directed 150° from the horizontal. What single force is the resultant force acting on the body?

Answer 1

`\beta= 51.65^(\circ)`

`F_r=19.35\ N`

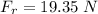
Step-by-step explanation:

Given:

• force acting to the horizontal right direction,
  `F_1=10\ lbf`

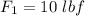
• force acting -135° to the horizontal,
  `F_2=25\ lbf`

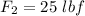
• force acting 150° to the horizontal,
  `F_3=5\ lbf`

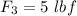
Now the total components of force in the horizontal direction:

`F_H=F_3\cos 150^(\circ)+F_2\cos(-135^(\circ))+10`

`F_H=5* cos150^(\circ)+25* cos(-135^(\circ))+10`

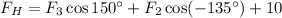
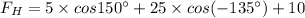
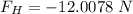`F_H=-12.0078\ N` -ve sign means acting in negative x-axis

The total vertical components in the vertical direction:

`F_v=5* sin150^(\circ)+25* sin(-135^(\circ))`

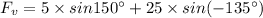
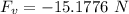`F_v=-15.1776\ N` -ve sign means acting in negative y-axis

Now the resultant:

`F_r=√(F_H^2+F_v^2)`

`F_r=√((-12.0078)^2+(-15.1776)^2)`

`F_r=19.35\ N`

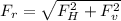
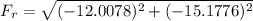
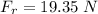
The angle of the force:

`tan\ \beta=(F_v)/(F_H)`

`tan\ \beta=(-15.1776)/(-12.0078)`

`\beta= 51.65^(\circ)`