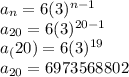Question

The sequence 6, 18, 54, 162, … shows the number of pushups Kendall did each week, starting

with her first week of exercising.
(a) Is this an arithmetic or geometric sequence?
(b) How can you find the next number in the sequence?
(c) Give the rule you would use to find the 20th week. Find the 20th week. (Show your work)

Answer 1

a) The given sequence is geometric.

b) The next term in the sequence is 486

c) The rule is:
`a_n=6(3)^(n-1)`

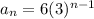
The 20th week will be: a_{20}=6973568802

Explanation:

The sequence 6, 18, 54, 162, … shows the number of push ups Kendall did each week, starting with her first week of exercising.

Part a) Is this an arithmetic or geometric sequence?

An arithmetic sequence is one, where difference between two consecutive terms is constant.

In the given sequence 6, 18, 54, 162,

18-6 = 12

54-18= 36

The difference is not constant so, the sequence is not arithmetic.

A geometric sequence is one, where ratio between two consecutive terms is constant.

In the given sequence 6, 18, 54, 162,

18/6 = 3

54/18 = 3

162/54 = 3

The ratio is constant so, the sequence is geometric.

The given sequence is geometric.

Part b) How can you find the next number in the sequence?

We can find next number in the sequence by using formula:

`a_n=a(r)^(n-1)`

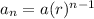
where a_n= nth term

a= first term

r= common ratio

The next term will be 5th term of the sequence.

Finding 5th term:

`a_n=a(r)^(n-1)\\a_5=6(3)^(5-1)\\a_5=6(3)^4\\a_5=6*81\\a_5=486`

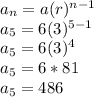
So, the next term in the sequence is 486

Part c) Give the rule you would use to find the 20th week. Find the 20th week

The rule used to find 20th week would be:

`a_n=6(3)^(n-1)`

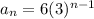
Here n=20

Finding 20th week

`a_n=6(3)^(n-1)\\a_(20)=6(3)^(20-1)\\a_(20)=6(3)^(19)\\a_(20)=6973568802`