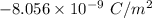Question

An electron in a vacuum chamber is fired with a speed of 9800 km/s toward a large, uniformly charged plate 75 cm away. The electron reaches a closest distance of 15 cm before being repelled.

Answer 1

The plate's surface charge density is
`-8.056*10^(-9)\ C/m^2`

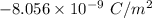
Step-by-step explanation:

Given that,

Speed = 9800 km/s

Distance d= 75 cm

Distance d' =15 cm

Suppose we determine the plate's surface charge density?

We need to calculate the surface charge density

Using work energy theorem

`W=\Delta K.E`

`W=(1)/(2)mv_(f)^2-(1)/(2)mv_(i)^2`

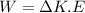
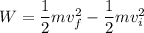
Here, final velocity is zero

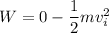`W=0-(1)/(2)mv_(i)^2`...(I)

We know that,

`W=-Fd`

`W=-E* e* d`

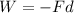
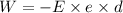
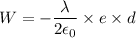`W=-(\lambda)/(2\epsilon_(0))* e* d`...(II)

From equation (I) and (II)

`-(1)/(2)mv_(i)^2=-(\lambda)/(2\epsilon_(0))* e* d`

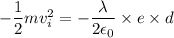
Charge is negative for electron

`\lambda=(mv^2\epsilon_(0))/((-e)d)`

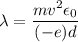
Put the value into the formula

`\lambda=-(9.1*10^(-31)*(9800*10^(3))^2*8.85*10^(-12))/(1.6*10^(-19)*(75-15)*10^(-2))`

`\lambda=-8.056*10^(-9)\ C/m^2`

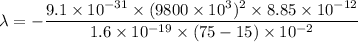
Hence, The plate's surface charge density is
`-8.056*10^(-9)\ C/m^2`