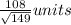Question

Find the area of triangle ABC with vertices A(2,1), B (12,2), C (12,8). Hence, or otherwise find the perpendicular distance from B to AC.

Answer 1

The area of a triangle is =54 square units

The perpendicular distance from B to AC is =
`(108)/(√(149) ) units`

Explanation:

Given a triangle ABC with vertices A(2,1),B(12,2) and C(12,8)

`x_1=2,y_1=1,x_2=12,y_2=2,x_3=12 and y_3=8`

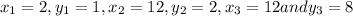
The area of a triangle is=
`(1)/(2) [x_1(y_2-y_3) +x_2 (y_3- y_1)+x_3(y_1-y_2)]`

=
`|(1)/(2) [2(2-8+12(8-1)+12(1-2)]|`

=
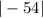`|-54|` = 54 square units

The length of AC =
`\sqrt{(x_1-x_3)^(2) +(y_1-y_3)^2}`

=
`\sqrt{(2-12)^(2) +(1-8)^2}`

=
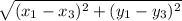
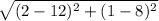
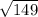`√(149)` units

Let the perpendicular distance from B to AC be = x

According To Problem

`(1)/(2) * x * √(149) = 54`

⇔
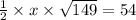
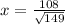`x =(108)/(√(149) )` units

Therefore the perpendicular distance from B to AC is =
`(108)/(√(149) ) units`