Question

Oil is leaking out of a ruptured tanker at the rate of r(t)=30e^(?0.09t) thousand liters per minute.

A. At what rate, in thousands of liters per minute, is the oil leaking out
at t=0? rate =
at t=60? rate =

B. How many thousands of liters leak out during the first hour?
Number of liters =

Answer 1

A)

At t = 0, oil is leaking out of a ruptured tanker at the rate of 30 thousand liters per minute.

At t = 60, oil is leaking out of a ruptured tanker at the rate of 0.1355 thousand liters per minute.

B)

331.82 thousands of liters leak out during the first hour.

Explanation:

The oil leakage rate, in thousand liters per minute, is:

`r(t) = 30e^(-0.09t)`

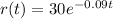
A. At what rate, in thousands of liters per minute, is the oil leaking out

At t = 0:

This is r(0)

`r(t) = 30e^(-0.09t)`

`r(0) = 30e^(-0.09*0) = 30`

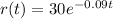
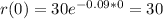
At t = 0, oil is leaking out of a ruptured tanker at the rate of 30 thousand liters per minute.

At t = 60:

This is r(60)

`r(t) = 30e^(-0.09t)`

`r(60) = 30e^(-0.09*60) = 0.1355`

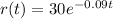
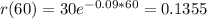
At t = 60, oil is leaking out of a ruptured tanker at the rate of 0.1355 thousand liters per minute.

B. How many thousands of liters leak out during the first hour?

r(t) is in thousand liters per minute.

Each hour has 60 minutes.

So the answer to this question is the integral from 0 to 60 of r(t).

Integral of the exponential function

`\int {e^(at)} \, dt = (e^(at))/(a)`

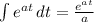
So

`\int\limits^(60)_0 {r(t)} \, dt`

`\int\limits^(60)_0 {30e^(-0.09t)} \, dt`

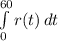
`-333.33e^(-0.09t)`, from t = 0 to t = 60.

This is

`-333.33e^(-0.09*60) - (-333.33e^(-0.09*0)) = 331.82`

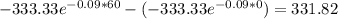
331.82 thousands of liters leak out during the first hour.