Question

If He gas has an average kinetic energy of 5930 J/mol under certain conditions, what is the root mean square speed of F2 gas molecules under the same conditions

Answer 1

To solve this problem we will apply the concept related to kinetic energy based on the ideal gas constant and temperature. From there and with the given values we will find the temperature of the system. As the temperature is the same it will be possible to apply the root mean square speed formula that is dependent on the element's molar mass, the ideal gas constant and the temperature, this would be:

`KE = (3)/(2) RT`

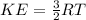
Where,

KE = Average kinetic energy of an ideal gas

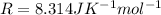`R = 8.314JK^(-1)mol^(-1)`= Ideal gas constant

T = Temperature

Replacing we have,

`KE = (3)/(2) RT`

`5930J/mol = (3)/(2)(8.314JK^(-1)mol^(-1))T`

`T = 475.503K`

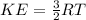
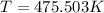
Therefore the temperature is 475.5K

RMS velocity of
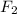`F_2` gas is

`v_(rms) = \sqrt{(3RT)/(M)}`

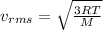
Where,

M = Molar mass of
`F_2`

`M = 38.00g/mol`

`M = 38.00*10^(-3) kg/mol`

`T = 475.5K`

`R = 8.314JK^(-1)mol^(-1)`

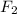
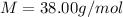
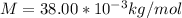
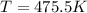
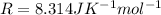
Replacing we have,

`v_(rms) = \sqrt{(3RT)/(M)}`

`v_(rms) = \sqrt{(3(8.314JK^(-1)mol^(-1))(475.5K ))/(38.00*10^(-3) kg/mol)}`

`v_(rms) = 558.662m/s`

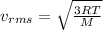
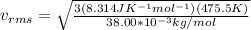
Therefore, the RMS velocity of
`F_2` gas is 558.6m/s