Question

Which of the following describes the transformation of g (x) = 3 (2) Superscript negative x Baseline + 2 from the parent function f (x) = 2 Superscript x? reflect across the x-axis, stretch the graph vertically by a factor of 3, shift 2 units up reflect across the y-axis, stretch the graph vertically by a factor of 2, shift 3 units up reflect across the x-axis, stretch the graph vertically by a factor of 2, shift 3 units up reflect across the y-axis, stretch the graph vertically by a factor of 3, shift 2 units up

Answer 1

it is d in edge

Answer 2

Reflect across the y-axis.

Stretch by a factor of 3.

Shift 2 units up.

Explanation:

Below are some transformations for a function
`f(x)` :

1. If
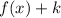`f(x)+k`, the function is shifted "k" units up.

2. If
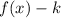`f(x)-k`, the function is shifted "k" units down.

3. If
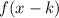`f(x-k)`, the function is shifted "k" units right.

4. If
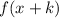`f(x+k)`, the function is shifted "k" units left.

5. If
`-f(x)`, the function is reflected over the x-axis.

6. If
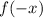`f(-x)`, the function is reflected over the y-axis.

7. If
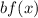`bf(x)` and
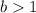`b>1`, the function is stretched vertically by a factor of "b".

8. If
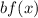`bf(x)` and
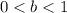`0<b<1` the function is compressed vertically by a factor of "b".

Then, given the parent function
`f(x)` :

`f(x)=2^x`

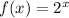
And knowing that the other function is:

`g(x)=3(2)^(-x)+2`

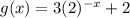
You can identify that the function
`g(x)` is obtained by:

- Reflecting the function
`f(x)` across the y-axis.

- Stretching the function
`f(x)` vertically by a factor of 3.

- Shifting the function
`f(x)` 2 units up.