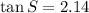Question

Find the tangent of S.

Answer 1

Therefore,

`\tan S=2.14`

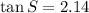
Explanation:

Given:

ΔSRQ is a Right angle triangle at ∠R = 90°

SR = 36 ....Adjacent side of ∠S

RQ = 77 ...Opposite side of ∠S

To Find:

`\tan S=?`

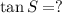
Solution:

ΔSRQ is a Right angle triangle at ∠R = 90° ..Given

By Tangent Identity we have

`\tan S = \frac{\textrm{side opposite to angle S}}{\textrm{side adjacent to angle S}}`

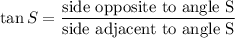
Substituting the values we get

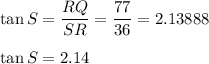`\tan S = (RQ)/(SR)=(77)/(36)=2.13888\\\\\tan S=2.14`...Rounded to the nearest hundredth

Therefore,

`\tan S=2.14`