Question

What is the decimal representation of the following signed binary numbers?

10000000
11001100
10110111

Answer 1

To convert signed binary numbers to their decimal representation, check if the first bit is 1 (indicating a negative number) and then find the two's complement of the rest of the bits. After converting the two's complement to decimal, prefix the number with a negative sign. For example, 10000000 represents -128, 11001100 represents -52, and 10110111 represents -73 in decimal.

Step-by-step explanation:

The question asks about converting signed binary numbers into their decimal representations. Signed binary numbers use the leftmost bit as a sign indicator, where 0 usually means positive and 1 means negative. To convert them into decimals, one must understand two's complement notation, which is a method used to represent negative binary numbers.

Steps for converting signed binary numbers to decimal:

1. Check the first bit (most significant bit). If it is 0, the number is positive. If it is 1, the number is negative and you will proceed with finding the two's complement of the rest of the bits.
2. To find the two's complement, invert all the bits (change 1s to 0s and vice versa) and then add 1 to the least significant bit.
3. Convert the resulting binary number to a decimal number.
4. If the original most significant bit was 1, prefix the result with a negative sign to show it is a negative decimal number.

Following these steps:

• 10000000: This represents -128 in decimal as it is the two's complement of 128 (the most significant 1 indicates a negative number).
• 11001100: The first bit is 1, so this is a negative number. Its two's complement is 00110100, which is 52 in decimal, thus the original number is -52.
• 10110111: The first bit is 1, so this is a negative number. Its two's complement is 01001001, which is 73 in decimal, thus the original number is -73.

Answer 2

(10000000)₂ = -128 in decimal

(11001100)₂ = -52 in decimal

(10110111)₂ = -73 in decimal

Step-by-step explanation:

NOTE: If Most Significant Bit is 0, it is positive number and if MSB is 1, it is negative number. If number is positive we can simply convert it to decimal. But if number is negative, follow following formula:

• (complement of the number) +1

EXAMPLE 1

(10000000)₂

(01 1 1 1 1 1 1)₂ ↔ complement of the number

+ 1

(10000000)₂ = 1 ×
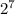`2^(7)`= 128 (magnitude in decimal)

But we remember MSB was 1 so answer is -128.

EXAMPLE 2

(1 1 0 0 1 1 00)₂

(0 0 1 1 0 0 1 1)₂

+ 1

(0 0 1 1 0 1 0 0)₂ = 52 (magnitude in decimal)

But we remember MSB was 1 so answer is -52.

EXAMPLE 3

(1 0 1 1 0 1 1 1)₂

(0 1 00 1 000)₂

+ 1

(01 00 1 00 1‬)₂ = 73 (magnitude in decimal)

But we remember MSB was 1 so answer is -73.