Question

I NEED HELP WITH THIS PROBLEM ASAP PLEASE!! THANK YOU VERY MUCH!! <3

Answer 1

OPTION C

OPTION E

Explanation:

Distributive property of Addition:

a(b + c) = ab + bc

In other words, 'a' is distributed over 'b' and 'c'.

Also, note that a mixed fraction, of the form
`$ \textbf{c} \frac{\textbf{x}}{\textbf{y}} = \textbf{c} + \frac{\textbf{x}}{\textbf{y}} $`

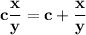
If a mixed fraction is of the type
`$ \textbf{-p}\frac{\textbf{q}}{\textbf{r}} \hspace{1mm} \textbf{=} \hspace{1mm} \textbf{-(p + } \frac{\textbf{q}}{\textbf{r}}) \hspace{1mm} \textbf{=} \hspace{1mm} \textbf{-p} \hspace{1mm} \textbf{-} \hspace{1mm} \frac{\textbf{q}}{\textbf{r}} $`

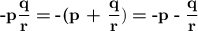
OPTION A:

`\textbf{3} \bigg ( \textbf{-4} \frac{\textbf{1}}{\textbf{2}} \bigg )`

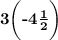
This can be written as:
`$ 3 \bigg ( - 4 - (1)/(2) \bigg ) $`

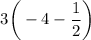
Now, we distribute 3 over -4 and
`$ -(1)/(2) $`.

`$ = 3(-4) + 3\bigg (-(1)/(2) \bigg ) $`

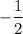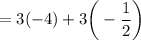
Therefore, OPTION A is incorrect.

OPTION B:
`$ \textbf{2} \frac{\textbf{1}}{\textbf{4}} \bigg ( \textbf{1} \frac{\textbf{3}}{\textbf{4}} \bigg ) $`

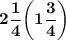
Now, this is written as:
`$ 2 + (1)/(2) \bigg ( 1 + (3)/(4) \bigg ) $`

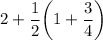
We have distribute 2 and
`$ (1)/(2) $` separately over 1 and
`$ (3)/(4) $`.

So, we should have
`$ 2 (1) + 2 \bigg ( (3)/(4) \bigg ) + (1)/(2) (1) + (1)/(2). (3)/(4) $`

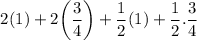
So, OPTION B is incorrect.

OPTION C:
`$ \textbf{-4} \bigg( - 5 \frac{\textbf{1}}{\textbf{3}} \bigg ) $`

`$ = - 4 \bigg ( -5 - (1)/(3) \bigg) $`

`$ = -4(-5) + (-4) \bigg (- (1)/(3) \bigg ) $`

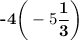
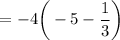
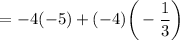
Hence, OPTION C is correct.

Similar method will help us know that OPTION D has used the Distributive property incorrectly and OPTION E has.

So, the answers are:

OPTION A

OPTION C

OPTION E