Question

Lisa is choosing between two exercise routines. In Routine #1, she does only running, burning 8.5 calories per minute. In Routine #2, she burns 28 calories walking. She then runs at a rate that burns 2.9 calories per minute. For what amounts of time spent running will Routine #1 burn at most as many calories as Routine #2? Use t for the number of minutes spent running, and solve your inequaliy for t

Answer 1

For at most 5 minutes spent on running burning calories in Routine #1 will be at most to Routine #2.

Explanation:

Given:

Let the number of minutes spent on running be 't'.

For Routine #1:

Calories burn each minute on running = 8.5

Total calories burn will be equal to Calories burn each minute on running multiplied by the number of minutes spent on running.

framing in equation form we get;

Total calories burn in Routine #1 =
`8.5t`

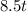
For Routine #2:

Calories burn in walking = 28 calories

Calories burn each minute on running = 2.9

Total calories burn will be equal to sum of Calories burn in walking and Calories burn each minute on running multiplied by the number of minutes spent on running.

framing in equation form we get;

Total calories burn in Routine #2 =
`28+2.9t`

We need to find amounts of time spent running will Routine #1 burn at most as many calories as Routine #2.

So we can say that;

Total calories burn in Routine #1
`\leq` Total calories burn in Routine #2

`8.5t\leq 28+2.9t`

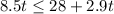
Combining like terms we get;

`8.5t-2.9t\leq 28\\\\5.6t\leq 28`

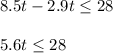
Dividing both side by 5.6 we get;

`(5.6t)/(5.6)\leq (28)/(5.6)\\\\t\leq 5\ mins`

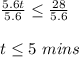
Hence For at most 5 minutes spent on running burning calories in Routine #1 will be at most to Routine #2.