Question

A satellite in a circular orbit 1250 kilometers above Earth makes one complete revolution every 110 minutes. What is its linear speed? Assume that Earth is a sphere of radius 6378 kilometers.

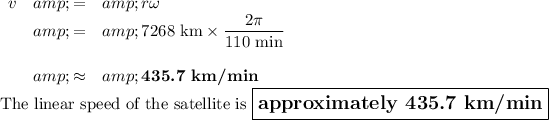
Answer 1

`\large \boxed{\text{approximately 435.7 km/min}}`

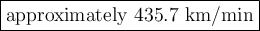
Explanation:

1. Angular speed

The angular speed ω is the angle θ swept out by the satellite in a given time t.

`\omega = (\theta)/(t) = \frac{2\pi}{\text{110 min}}`

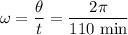
2. Linear speed

The formula for the linear speed v is

v = rω, where

r = the distance from the centre of the Earth = 6378 km + 1250 km = 7628 km

`\begin{array}{rcl}v & = & r\omega\\& = & \text{7268 km} * \frac{2\pi}{\text{110 min}}\\\\& \approx & \textbf{435.7 km/min}\\\end{array}\\\text{The linear speed of the satellite is $\large \boxed{\textbf{approximately 435.7 km/min}}$}`