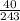Question

Please help ! Geometric sequences!

Answer 1

The next fraction in the given geometric sequence is
`(40)/(243)`

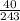
Therefore
`a_5=(40)/(243)`

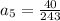
Explanation:

Given geometric sequence is

`(5)/(6), (5)/(9), (10)/(27), (20)/(81), \ldots`

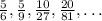
To find the 5th term of the given geometric sequence:

Let
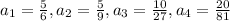`a_1=(5)/(6), a_2=(5)/(9), a_3=(10)/(27), a_4=(20)/(81)` etc.

First find the common ratio

`r=(a_2)/(a_1)`

`=((5)/(9))/((5)/(6))`

`=(5)/(9)* (6)/(5)`

Therefore
`r=(2)/(3)`

`r=(a_3)/(a_2)`

`=((10)/(27))/((5)/(9))`

`=(10)/(27)* (9)/(5)`

Therefore
`r=(2)/(3)`

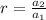
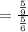
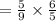
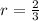
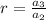
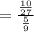
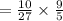
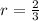
Therefore the common ratio
`r=(2)/(3)`

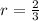
The nth term of geometric sequence is
`a_n=a_1r^(n-1)`

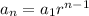
Put
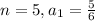`n=5, a_1=(5)/(6)` and
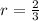`r=(2)/(3)` in the above equation we get

`a_5=(5)/(6)((2)/(3))^(5-1)`

`=(5)/(6)((2)/(3))^4`

`=(5)/(6)((2)/(3)* (2)/(3)* (2)/(3)* (2)/(3))`

`=(5)/(3)((8)/(81))`

`a_5=(40)/(243)`

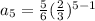
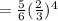
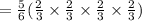
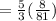
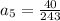
Therefore
`a_5=(40)/(243)`

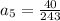
Therefore the next fraction in the given geometric sequence is
`(40)/(243)`