There are 14 dimes and 19 nickels
Solution:
Let "d" be the number of dimes
Let "n" be the number of nickels
A nickel is worth 5 cents and a dime worth 10 cents
She has 33 coins in all
Therefore, number of dimes + number of nickels = 33
d + n = 33
d = 33 - n ----------- eqn 1
Ayana has 2.35 in nickels and dimes
$ 2.35 is equal to 235 cents
Therefore, we frame a equation as:
number of dimes x 10 cents + number of nickels x 5 cents = 235
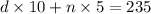
10d + 5n = 235 ----------- eqn 2
Substitute eqn 1 in eqn 2
10(33 - n) + 5n = 235
330 - 10n + 5n = 235
5n = 330 - 235
5n = 95
n = 19
Substitute n = 19 in eqn 1
d = 33 - 19
d = 14
Thus there are 14 dimes and 19 nickels