Answer:
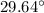
Step-by-step explanation:
The expression to calculate the angle
 of an ideally banked curve in which friciton is not needed is:
of an ideally banked curve in which friciton is not needed is:
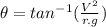
Where:
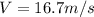 is the car's velocity
is the car's velocity
 is the radius of the curve
is the radius of the curve
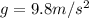 is the acceleration due gravity
is the acceleration due gravity
As you may see, this angle does not depend on the mass of the car.
Solving with the given values:

Finally:
