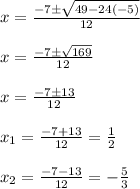Question

It is known that x1 and x2 are roots of the equation
`6x^(2) +7x+k=0`

, where
`2x_(1) +3x_(2) =-4`. Find k.

Answer 1

`k=-5`

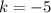
Explanation:

we know that

The formula to solve a quadratic equation of the form

`ax^(2) +bx+c=0`

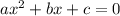
is equal to

`x=\frac{-b\pm\sqrt{b^(2)-4ac}} {2a}`

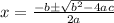
in this problem we have

`6x^(2) +7x+k=0`

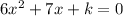
so

`a=6\\b=7\\c=k`

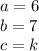
substitute in the formula

`x=\frac{-7\pm\sqrt{7^(2)-4(6)(k)}} {2(6)}\\\\x=\frac{-7\pm√(49-24k)} {12}`

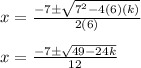
so

`x_1=\frac{-7+√(49-24k)} {12}\\\\x_2=\frac{-7-√(49-24k)} {12}`

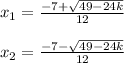
Remember that

`2x_1+3x_2=-4`

substitute

`2(\frac{-7+√(49-24k)} {12})+3(\frac{-7-√(49-24k)} {12})=-4\\\\(\frac{-14+2√(49-24k)} {12})+(\frac{-21-3√(49-24k)} {12})=-4`

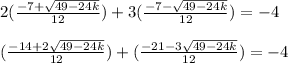
Multiply by 12 both sides

`(-14+2√(49-24k))+(-21-3√(49-24k))=-48\\\\-35-√(49-24k)=-48\\\\√(49-24k)=48-35\\\\√(49-24k)=13`

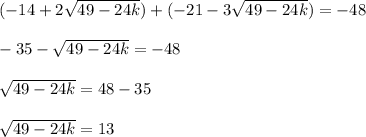
squared both sides

`49-24k=169\\24k=49-169\\24k=-120\\k=-5`

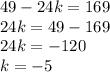
therefore

The equation is

`6x^(2) +7x-5=0`

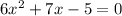
The roots are

`x=\frac{-7\pm√(49-24(-5))} {12}\\\\x=\frac{-7\pm√(169)} {12}\\\\x=\frac{-7\pm13} {12}\\\\x_1=\frac{-7+13} {12}=\frac{1} {2}\\\\x_2=\frac{-7-13} {12}=-\frac{5} {3}`