Question

Help?????? I have two of these that need answering. ​

Answer 1

The value of 'x' is 7 that will make make L║M.

Explanation:

Given,

Line segment L and line segment M are cut by a transversal line.

We can name it as 't' transversal line and also the given angle measures as ∠1 and ∠2.

So, ∠1 =
`7x+9`

∠2 =
`8x+2`

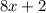
We have to find the value of 'x'.

Solution,

Since L and M are two line segment which is cut by another line segment 't'.

For L║M, the measure of ∠1 and ∠2 must be equal according to corresponding angle property.

"When the measure of a pair of same side corresponding angle is equal, then the line segments are parallel".

`\therefore \angle1=\angle2`

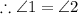
On substituting the values, we get;

`7x+9=8x+2`

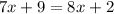
Combining the like terms, we get;

`8x-7x=9-2\\\\x=7`

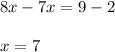
Now we will find out the measure of ∠1 and ∠2.

`\angle1=7x+9=7*7+9=49+9 =58`

`\angle2=8x+2=8*7+2=56+2=58`

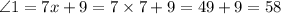
Hence The value of 'x' is 7 that will make make L║M.