Answer:
The volume of radius is
 × π × radius³ Proved
× π × radius³ Proved
Step-by-step explanation:
Given as :
We know that volume of sphere is v =
 × π × radius³
× π × radius³
Or, v =
 × π × r³
× π × r³
Let prove the volume of sphere
So, From the figure of sphere
At the height of z , there is shaded disk with radius x
Let Find the area of triangle with side x , z , r
From Pythagorean theorem
x² + z² = r²
Or, x² = r² - z²
Or, x =

Now, Area of shaded disk = Area = π × x²
Where x is the radius of disk
Or, Area of shaded disk = π × (
 ) ²
) ²
∴ Area of shaded disk = π × (r² - z²)
Again
If we calculate the area of all horizontal disk, we can get the volume of sphere
So, we simply integrate the area of all disk from - r to + r
i.e volume =
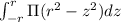
Or, v =
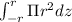 -
-

Or, v = π r² (r + r) - π
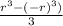
Or, v = π r² (r + r) - π
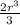
Or, v = 2πr³ - π
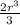
Or, v = 2πr³ (
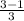 )
)
Or, v = 2πr³ ×

∴ v =
 × π × r³
× π × r³
Hence, The volume of radius is
 × π × radius³ Proved . Answer
× π × radius³ Proved . Answer