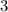How does h(x) = 3x - 8 change over the interval from x =3 to x=4

Question

asked Apr 9, 2021 40.6k views

1 Answer

Hrokr · Answer 1 · 2021-04-14T06:12:15+0000

Answer:

The average rate of change of the function
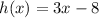h(x) = 3x - 8 over the interval
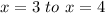$x =3\ to\ x=4$ is

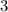
Explanation:

Given function is
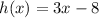
h(x) = 3x - 8

Let
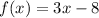
f(x) = 3x - 8

And the interval is
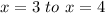
$x =3\ to\ x=4$

The average rate of change of the function over the interval to is given by

The average rate of change
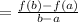
=(f(b)-f(a))/(b-a)

Plug the value in the equation we get,

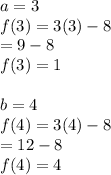
$a=3\\f(3)=3(3)-8\\=9-8\\f(3)=1\\\\b=4\\f(4)=3(4)-8\\=12-8\\f(4)=4$

The average rate of change

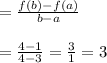
$=(f(b)-f(a))/(b-a)\\\\=(4-1)/(4-3)=(3)/(1)=3$

So, the average rate of change of the function
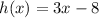h(x) = 3x - 8 over the interval
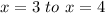$x =3\ to\ x=4$ is